Příklad 301
Ve třídě je 35 žáků. 20 z nich navštěvuje matematický kroužek, 11 fyzikální a 10 žáků nenavštěvuje žádný z těchto kroužků. Kolik žáků navštěvuje matematický i fyzikální kroužek? Kolik jich navštěvuje jen matematický kroužek?
| Řešení | Ukázat |
|---|---|
Příklad 302
V oddělení výzkumného ústavu pracuje několik osob, z nichž každá zná alespoň jeden z těchto tří světových jazyků - angličtinu, němčinu nebo francouzštinu. Šest osob ovládá angličtinu, šest němčinu a sedm francouzštinu. Čtyři osoby hovoří anglicky i německy, 3 osoby německy i francouzsky a 2 osoby francouzsky i anglicky. Všechny tři jazyky ovládá jedna osoba. Kolik osob pracuje v oddělení?
| Řešení | Ukázat |
|---|---|
Příklad 303
V oddělení ústavu pracuje několik osob, z nichž každá ovládá aspoň jeden cizí jazyk: 7 osob ovládá angličtinu, 7 němčinu, 1 španělštinu, 8 francouzštinu, 5 umí německy a anglicky, 4 německy a francouzsky, 3 francouzsky a anglicky, 1 španělsky a německy, 1 španělsky a anglicky, 1 španělsky a francouzsky, 2 umí německy, francouzsky, anglicky, 1 umí španělsky, německy, anglicky, 1 španělsky, francouzsky, německy, 1 španělsky, francouzsky, anglicky a 1 osoba ovládá všechny 4 jazyky. Určete, kolik osob pracuje v ústavu?
| Řešení | Ukázat |
|---|---|
Příklad 304
Zkoušku, která se skládala ze tří příkladů psalo 120 studentů. 1. příklad vyřešilo 55 studentů, druhý 44 a třetí 34. Všechny tři příklady vyřešilo 12 studentů a právě dva příklady 25 studentů. Kolik studentů nevyřešilo ani jeden příklad?
| Řešení | Ukázat |
|---|---|
Příklad 305
V ročníku je 200 studentů. 100 z nich udělalo zkoušku z matematiky (M), 150 z fyziky (F) a 175 z češtiny (Č). M i F udělalo 75 studentů, M i Č 80 studentů a F a Č udělalo 130 studentů. Jaký je nejvyšší možný počet studentů, kteří neudělali ani jednu zkoušku? Kolik nejméně a nejvíce studentů udělalo všechny zkoušky?
| Řešení | Ukázat |
|---|---|
Příklad 306
Kolik existuje přirozených čísel menších nebo rovnajících se 100, která nejsou dělitelná žádným z čísel 2, 3, 5?
| Řešení | Ukázat |
|---|---|
Příklad 307
Kolik existuje kladných celých čísel menších než 420, která nejsou dělitelná žádným z čísel 2, 5, 7?
| Řešení | Ukázat |
|---|---|
Příklad 308
Kolik prvků množiny  není dělitelných ani 2, ani 5, ani 7, ani 11?
není dělitelných ani 2, ani 5, ani 7, ani 11?
| Řešení | Ukázat |
|---|---|
Příklad 309
Určete počet přirozených čísel menších než 210, která jsou nesoudělná s číslem 210.
| Řešení | Ukázat |
|---|---|
Příklad 310
Osm dětí hraje hru, při níž se dobrovolně rozdělí na SKŘÍTKY, ČARODĚJE a OBRY. Aby se hra mohla uskutečnit, musí být pro každou roli aspoň jeden adept. Jaký je počet všech možných rozdělení vhodných pro tuto hru?
| Řešení | Ukázat |
|---|---|
Příklad 311
Určete kolik existuje možností, jak rozdělit 20 zaměstnanců do tří dílen tak, aby byl splněn předpis, že v žádné dílně, pokud se v ní pracuje, nesmí nikdo pracovat sám.
| Řešení | Ukázat |
|---|---|
Příklad 312
Šestnáct chlapců máme rozdělit do dvou družstev po osmi. Kolika způsoby to můžeme udělat, jestliže Martin chce být s Petrem v jednom družstvu, Jirka s Tomášem v jednom družstvu a Honza nechce být v jednom družstvu s Karlem? Všichni chlapci mají různá jména.
| Řešení | Ukázat |
|---|---|
Příklad 313
Kolika způsoby můžeme posadit do řady 3 Angličany, 3 Francouze a 3 Turky, tak aby žádní tři krajané neseděli vedla sebe?
| Řešení | Ukázat |
|---|---|
Příklad 314
Kolika způsoby lze seřadit do fronty 5 Čechů, 4 Maďary a 3 Rusy tak, aby žádní příslušníci téhož národa netvořili jeden souvislý blok?
| Řešení | Ukázat |
|---|---|
Příklad 315
Určete, kolik je takových permutací 6-prvkové množiny 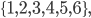 které nemají ani jeden prvek na stejném místě jako v základním uspořádání "123456".
které nemají ani jeden prvek na stejném místě jako v základním uspořádání "123456".
| Řešení | Ukázat |
|---|---|
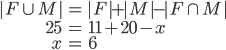
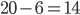
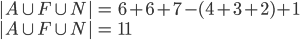
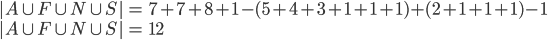
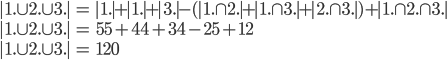

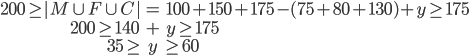
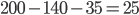
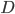
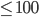
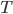
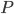
![|D|=[\frac{100}2]=50](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_13f5926198359cbf8c10b0330163108b.gif)
![[x]](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_3e5314e9fd31509fdeb83faa0f729ba2.gif)
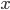
![|T|=[\frac{100}3]=33](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_7a247f4c737548b57e5fb6e711abafb7.gif)
![|P|=[\frac{100}5]=20](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_0ef9e075e5f6dbf5aab877d6b0c47c1e.gif)
![|D\cap T|=[\frac{100}6]=16](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_500d339acf7ea0a38983dfba78d1a974.gif)
![|D\cap P|=[\frac{100}{10}]=10](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_36ec9f66a5bc73aa0bf6d1fdaafdb053.gif)
![|T\cap P|=[\frac{100}{15}]=6](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_fc1c6ea3d86c7c7cc765f9a7428d3418.gif)
![|D\cap T\cap P|=[\frac{100}{30}]=3](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_c6b3742d0e41a5cdebf3a8252154e036.gif)
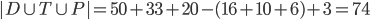
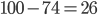
![|D|=[\frac{419}2]=209](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_5e46dc867c3c53023790c550d875a682.gif)
![|P|=[\frac{419}5]=83](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_6b5682243e7bc44e0381038b4cd5edf4.gif)
![|S|=[\frac{419}7]=59](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_68eaaf27b3c1ae08bee0f25df6ad8a92.gif)
![|D\cap P|=[\frac{419}{10}]=41](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_f55ea524b2c7d4a9da1e499cc52a62ae.gif)
![|D\cap S|=[\frac{419}{14}]=29](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_ddc74c6fb2298f5a68708580baa0ba97.gif)
![|P\cap S|=[\frac{419}{35}]=11](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_77b0247ad87d9294963ccebf72ae910f.gif)
![|D\cap P\cap S|=[\frac{419}{70}]=5](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_e30563e9b5ac6b575c793c0499d5749e.gif)
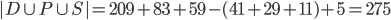
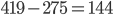
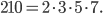
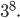
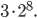
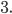
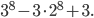
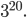
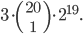
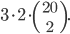
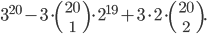
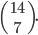
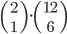
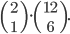

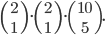
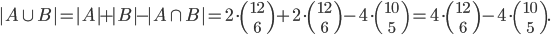
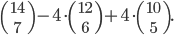
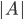
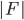
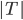
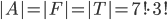
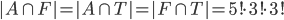
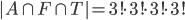
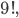
![9!-[3\cdot7!\cdot3!-3\cdot5!\cdot(3!)^2+(3!)^4]](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_7f127707f52f613dc87069a6351623b7.gif)
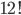
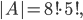
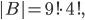
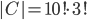
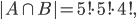
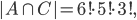
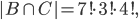
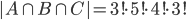
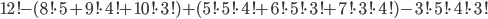
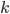
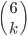

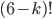
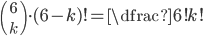
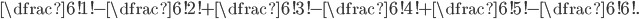
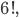
![6!-\left[\dfrac{6!}{1!}-\dfrac{6!}{2!}+\dfrac{6!}{3!}-\dfrac{6!}{4!}+\dfrac{6!}{5!}-\dfrac{6!}{6!}\right]](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_3e083bad8788c9092b7c811107d4bcb6.gif)