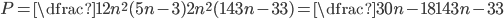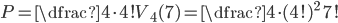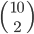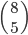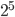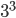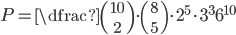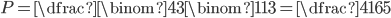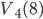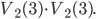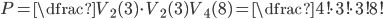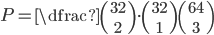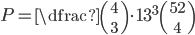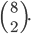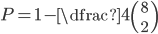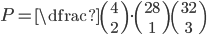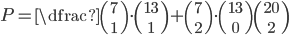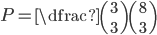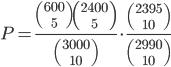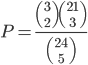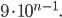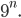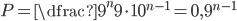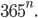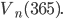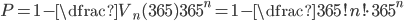Příklad 624
Na začátku hry obdržím 4 karty. Dostal jsem tři esa a jednoho krále (z normálního balíčku s 52 kartami).
(a) Obdržel jsem pátou kartu. Jaká je pravděpodobnost, že pátá karta bude král?
(b) Obdržel jsem pátou kartu. Jaká je pravděpodobnost, že pátá karta bude eso?
(d) Jaká je pravděpodobnost, že při rozdání 4 karet dostanu právě 3 stejné hodnoty?
| Řešení | Ukázat |
|---|---|
Příklad 625
V bedně je 36 červených míčů a 4 modré. Jaká je pravděpodobnost, že mezi devíti namátkou vybranými míči
(a) nebude modrý míč?
(b) budou právě 2 modré míče?
| Řešení | Ukázat |
|---|---|
Příklad 626
Devět lidí, včetně Alice, máme rozdělit do dvou rozlišitelných týmů po čtyřech plus rozhodčí. Jestliže jsou všechna rozdělení stejně pravděpodobná, jaka je pravděpodobnost, že bude Alice rozhodčí?
| Řešení | Ukázat |
|---|---|
Příklad 627
Z množiny všech desetibitových řetězců vybereme náhodně jeden. Jaká je pravděpodobnost, že součet jeho cifer bude sedm?
| Řešení | Ukázat |
|---|---|
Příklad 628
V balíčku je 52 karet a 13 z nich jsou srdce. Vyberu náhodně z balíčku 7 karet. Jaká je pravděpodobnost, že právě tří z nich budou srdce?
| Řešení | Ukázat |
|---|---|
Příklad 629
Na každé hraně dané krychle je dáno 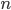 jejich vnitřních bodů, z nichž každé dva jsou navzájem různé, a jsou sestrojeny všechny trojúhelníky, jejichž vrcholy leží na uvedených bodech. Určete pravděpodobnost
jejich vnitřních bodů, z nichž každé dva jsou navzájem různé, a jsou sestrojeny všechny trojúhelníky, jejichž vrcholy leží na uvedených bodech. Určete pravděpodobnost 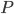 , že při náhodném výběru jednoho z daných trojúhelníků bude vybrán trojúhelník, ležící na povrchu krychle.
, že při náhodném výběru jednoho z daných trojúhelníků bude vybrán trojúhelník, ležící na povrchu krychle.
| Řešení | Ukázat |
|---|---|
Příklad 630
Čtyři osoby se mají posadit ke stolu, před nímž je řada sedmi židlí. Jaká je pravděpodobnost, že mezi nimi nebude prázdná židle, volí-li si svá místa zcela náhodně?
| Řešení | Ukázat |
|---|---|
Příklad 631
Máme jednu kostku a házíme desetkrát. Jaká je pravděpodobnost, že jsme hodili dvě jedničky, tři sudá čísla a pět pětek nebo trojek? Například výčet hodů 2461133553 vyhovuje.
| Řešení | Ukázat |
|---|---|
Příklad 632
Každé z písmen slova "MATHEMATICS" napíšeme na kartičku a dáme do osudí. Pak bez vracení vytáhneme 3 kartičky. Jaká je pravděpodobnost, že vytáneme tři samohlásky?
| Řešení | Ukázat |
|---|---|
Příklad 633
Z číslic 1, 1, 2, 2, 2, 3, 3, 3 postupně náhodně vybereme čtyři číslice a umístíme vedle sebe. Jaká je pravděpodobnost, že tímto způsobem dostaneme číslo 3223?
| Řešení | Ukázat |
|---|---|
Příklad 634
Náhodně vybíráme trojice polí na čtvercové šachovnici se 64 polí (32 polí bílých a 32 polí černých). Určete pravděpodobnost, že při jednom výběru vybereme takovou trojici polí, ve které budou právě dvě bílá pole.
| Řešení | Ukázat |
|---|---|
Příklad 635
Z balíčku 52 karet, kde jsou 4 barvy po 13 kartách, jsou hráči rozdány 4 karty. Jaká je pravděpodobnost, že každá karta bude jiné barvy?
| Řešení | Ukázat |
|---|---|
Příklad 636
Jaká je pravděpodobnost, že dva náhodně vybrané vrcholy krychle leží na stejné stěně?
| Řešení | Ukázat |
|---|---|
Příklad 637
Ze sady zamíchaných mariášových karet rozdáme 3. Jaká je pravděpodobnost, že jsme dostali právě dvě esa?
| Řešení | Ukázat |
|---|---|
Příklad 638
Zkouška má 20 otázek z nichž se losují 2. Josef se naučil prvních 7. Jaká je pravděpodobnost jevu, že aspoň jednu otázku bude umět?
| Řešení | Ukázat |
|---|---|
Příklad 639
V závodě startuje osm závodníků, mezi nimi Petr, Tomáš a Lukáš a jména závodníků se neopakují. Šance na výhru u všech zúčastněných je stejná. Jaká je pravděpodobnost, že se Petr, Tomáš a Lukáš podělí o medaile?
| Řešení | Ukázat |
|---|---|
Příklad 640
V tombole jee 3000 losů a z nich 600 výherních. Dorazí paní, která si koupí 10 losů a poté dorazí pán, který si také koupí 10 losů. Jaká je pravděpodobnost, že paní koupila 5 výherních losů a pán žádný?
| Řešení | Ukázat |
|---|---|
Příklad 641
Máme balíček 24 kartiček a z nich jsou tři modré. Náhodně vytáhneme 5 kartiček bez vracení. Jaká je pravděpodobnost, že právě dvě kartičky budou modré?
| Řešení | Ukázat |
|---|---|
Příklad 642
Určete pravděpodobnost, že 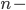 ciferné kladné číslo nebude mít žádné dvě za sebou jdoucí cifry stejné.
ciferné kladné číslo nebude mít žádné dvě za sebou jdoucí cifry stejné.
| Řešení | Ukázat |
|---|---|
Příklad 643
Určete pravděpodobnost, že v náhodně vybrané skupině 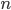 lidí
lidí 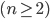 jsou aspoň, kteří mají narozeniny ve stejný den.
jsou aspoň, kteří mají narozeniny ve stejný den.
| Řešení | Ukázat |
|---|---|
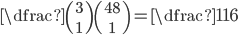
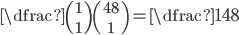
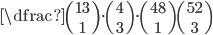
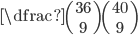
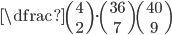
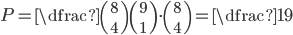
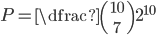
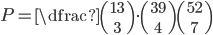
![6\left[{4n\choose3}-4{n\choose3}\right]=12n^2(5n-3)](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_118ad7d62244c569a846de12f591ac4e.gif)