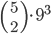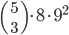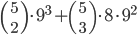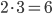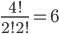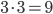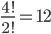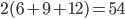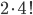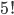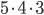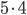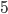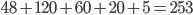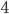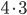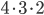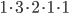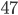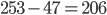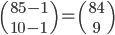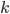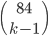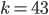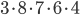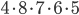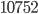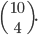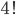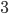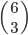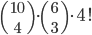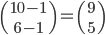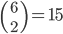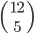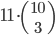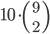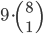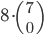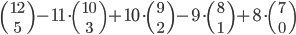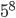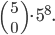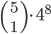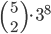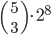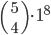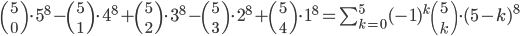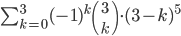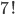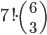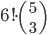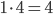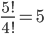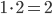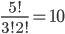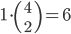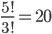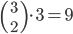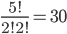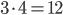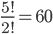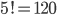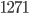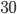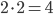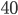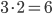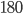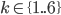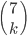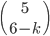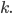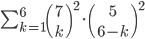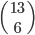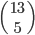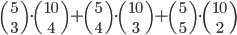Příklad 415
Kolik způsoby lze vytvořit 6-ti ciferné číslo tak, aby bylo sudé a žádné cifry se v něm neopakovaly?
| Řešení | Ukázat |
|---|---|
Příklad 416
Kolik čtyřciferných přirozených čísel lze vytvořit z číslic 0, 2, 5?
| Řešení | Ukázat |
|---|---|
Příklad 417
Tabulka na odpovědi u testu se skládá z 33 řádku (každý řádek odpovídá jedné otázce) s pěti čtverečky (každý odpovídá odpovědi). U každé otázky je potřeba vybrat jedno z pěti řešení, z nichž je právě jedno správné, a začernit odpovídající čtvereček. Některé otázky mohou zůstat bez odpovědi, ale není možné začernit více než jeden čtvereček v řádku. Za správnou odpěď je 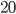 bodů, za špatnou
bodů, za špatnou 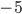 bodů a za neoznačené řešení
bodů a za neoznačené řešení 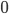 bodů.
bodů.
(a) Kolik obrazců takto může vzniknout?
(b) Kolik obrazců může vzniknout, když test byl ohodnocen 100 body?
| Řešení | Ukázat |
|---|---|
Příklad 418
Kolik existuje pětimístných přirozených čísel, která mají ve svem zápisu sudý počet sudých cifer?
| Řešení | Ukázat |
|---|---|
Příklad 419
Kolik existuje přirozených šesticiferných čísel, v jejichž zápisu jsou právě tři číslice 3?
| Řešení | Ukázat |
|---|---|
Příklad 420
Určete počet všech čtyřciferných čísel, dělitelných devíti, v jejichž dekadickém zápisu nejsou jiné číslice, než 0, 1, 2, 5, 7.
| Řešení | Ukázat |
|---|---|
Příklad 421
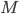 je množina všech přirozených čísel menších než
je množina všech přirozených čísel menších než 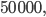 v jejichž dekadickém zápisu není žádná z číslic 0, 3, 4, 6, 8 a každá ze zbývajících je v něm nejvýše jednou. Určete počet sudých a lichých čísel v množině
v jejichž dekadickém zápisu není žádná z číslic 0, 3, 4, 6, 8 a každá ze zbývajících je v něm nejvýše jednou. Určete počet sudých a lichých čísel v množině 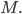
| Řešení | Ukázat |
|---|---|
Příklad 422
Kolika způsoby můžeme napsat číslo 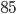
(a) jako součet 10 kladných sčítanců?
(b) Pro jaký počet kladných sčítanců je počet různých způsobů největší? Předpokládáme, že rozlišujeme pořadí sčítanců.
| Řešení | Ukázat |
|---|---|
Příklad 423
Najděte počet sudých čísel, která existují mezi čísly 10000 a 79999 a v nichž se žádná číslice neopakuje.
| Řešení | Ukázat |
|---|---|
Příklad 424
Kolik různých deseticiferných čísel můřeme vytvořit z cifer 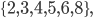 když
když
(a) se každá lichá cifra v čísle vyskytuje přesně 3 krát a každá sudá právě jednou?
(b) každá cifra je použita aspoň jednou a jsou seřazeny vzestupně?
| Řešení | Ukázat |
|---|---|
Příklad 425
Kolik různých součtů může padnout při hodu třemi kostkami, kde jedna je 6stěnná, druhá 8stěnná a třetí 12stěnná? Každá kostka je normálně číslována celými čísly od 1 do počtu stěn.
| Řešení | Ukázat |
|---|---|
Příklad 426
Kolik různých součtů lze hodit, pokud současně házíme jednou osmistěnnou a dvěma desetistěnnými kostkami?
| Řešení | Ukázat |
|---|---|
Příklad 427
V tenisovém klubu se sešlo 6 hráčů. V kolika dvojicích si mohou zahrát dvouhru?
| Řešení | Ukázat |
|---|---|
Příklad 428
Na poličce je 12 různých knih. Vybereme z nich 5 takových, že žádné dvě na poličce nestály vedle sebe. Kolika působy to lze udělat?
| Řešení | Ukázat |
|---|---|
Příklad 429
Osm lidí s řidičskýıni průkazy jede na výlet. Na výběr mají 5 různých aut a do každého vejde všech osm lidí. Kolika způsoby mohou obsadit auta, pokud žádné auto nesmí zůstat prázdné?
| Řešení | Ukázat |
|---|---|
Příklad 430
Byli jsme tři, kouřili před školou a trápili se představou, že kouření může přinášet vážně zdravotní komplikace. Tu přistoupil vysílený muž a rozdal nám 5 různých reklamních letáčků tak, aby měl každý z nás alespoň jeden. Kolika způsoby to mohl provést? Pokud někdo dostal více letáků, tak nerozlišujeme pořadí, ve kterěm je dostal.
| Řešení | Ukázat |
|---|---|
Příklad 431
Byli jsme čtyři, seděli v baru a popíjeli. Trápilo nás špatné svědomí, že místo abychom ve životě dělali něco pořádného, jsme závislí na alkoholu. Tu k nám přistoupil rozjařený barman a namíchal nám sedm různých drinků tak, aby každý dostal alespoň jeden. Kolika způsoby to mohl provést, jestliže rozlišujeme pořadí drinků, které jsme vypili.
| Řešení | Ukázat |
|---|---|
Příklad 432
Janě zbylo od narozenin 6 různých čokoládových bonbónů. Chce si je rozdělit na čtyři po sobě jdoucí dny tak, aby každý den snědla alespoň jeden. Kolik má možností, jestliže rozlišujeme pořadí, ve kterém bonbóny sní?
| Řešení | Ukázat |
|---|---|
Příklad 433
Ze slova ABRAKADABRA vybereme 5 písmen a z nich sestavíme nové slovo. Kolik takových slov můžeme vytvořit?
| Řešení | Ukázat |
|---|---|
Příklad 434
Ze slova MISSISSIPPI vybereme 5 písmen a z nich sestavíme nové slovo. Kolik takových slov můžeme vytvořit?
| Řešení | Ukázat |
|---|---|
Příklad 435
Manžel má 12 známých, z toho 5 žen a 7 mužů. Manželka 7 žen a 5 mužů. Kolika způsoby můžeme sestavit skupinu 6 mužů a 6 žen tak, aby 6 osob znal manžel a 6 manželka? Předpokládáme, že manžel a manželka nemají společné známé.
| Řešení | Ukázat |
|---|---|
Příklad 436
Z deseti mužů, mezi nimiž je pan Novák, a z pěti žen, mezi nimiž je paní Nováková, se má vytvořit sedmičlenná skupina. Určete počet způsobů, jimiž to lze provést, jestliže v teto skupině
(a) má být paní Nováková a nemá být pan Novák.
(b) má být paní Nováková i pan Novák.
(c) mají být aspoň tři ženy.
| Řešení | Ukázat |
|---|---|
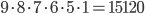
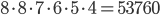
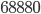
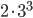
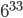
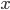
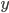
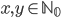
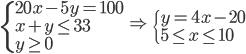
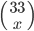
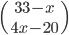
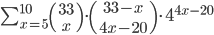
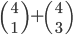
![4\cdot\left[{4\choose1}+{4\choose3}\right]\cdot5^4](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_494989c049bb2d03d9d1576d4dcaee3d.gif)
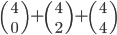
![5\cdot\left[{4\choose0}+{4\choose2}+{4\choose4}\right]\cdot5^4](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_84c0a85b9492312b15d2ef40e6d503ab.gif)
![4\cdot\left[{4\choose1}+{4\choose3}\right]\cdot5^4+5\cdot\left[{4\choose0}+{4\choose2}+{4\choose4}\right]\cdot5^4](http://kombinatorika.rubesz.cz/wp-content/plugins/latex/cache/tex_0c795705c5e9f38e7ec77edb6b136da3.gif)