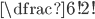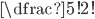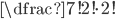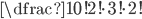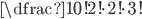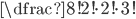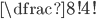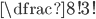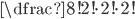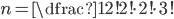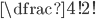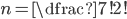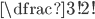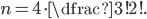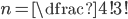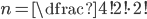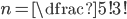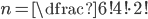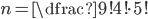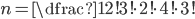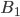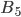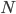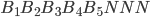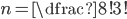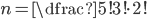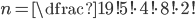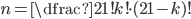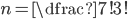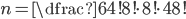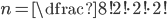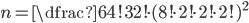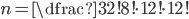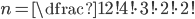Příklad 110
Kolik existuje anagramů slov:
| (a) OHRADA |
(b) TRUST |
| (c) OPOSSUM |
(d) MATEMATIKA |
| (e) BOOKKEEPER |
(f) TENNESSE |
| (g) CARAVANA |
(h) VEVERKA |
| (i) PARABOLA |
(j) HARAKIRI |
| Řešení |
Ukázat |
Ve všech případech určíme počet možností prostým dosazením do vztahu pro permutace s opakováním.
(a) 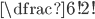 (b) 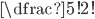 (c) 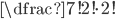 (d) 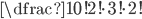 (e) 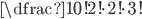 (f) 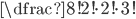 (g) 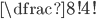 (h) 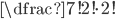 (i) 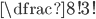 (j) 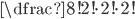
|
Příklad 111
Kolik existuje anagramů jména "BLAISE PASCAL" složených ze dvou šestipísmenných slov?
| Řešení |
Ukázat |
Protože počet anagramů bez mezery je stejný jako s mezerou uprostřed (prostě tam tu mezeru vložíme), je 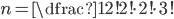
|
Příklad 112
Kolik existuje anagramů slova "PEŠEK" takových, že písmeno "Š" je uprostřed?
| Řešení |
Ukázat |
Na písmeno "Š" na chvíli zapomeneme - je uprostřed. Ostatní písmena můžeme přerovnat 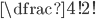 způsoby.
|
Příklad 113
Kolik existuje anagramů slova "DEFINICE", ve kterých obě "I" sousedí?
| Řešení |
Ukázat |
Obě "I" zabalíme do "balíku". Máme tak 7 objektů a "E" se opakuje dvakrát. 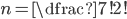
|
Příklad 114
Kolik existuje anagramů slova "FASETA" takových, že v nich zůstane zachované pořadí souhlásek a žádné dvě samohlásky nesousedí?
| Řešení |
Ukázat |
Rozmístíme si souhlásky: "_F_S_T_". Vzniknou 4 pozice pro samohlásky. Z těchto pozic můžeme vybrat 3, na něž umístíme samohlásky, čtyřmi způsoby (protože jsou 4 možnosti pro prázdnou pozici). Samohlásky pak můžeme přerovnat 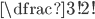 způsoby. Celkový počet anagramů je pak 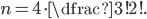
|
Příklad 116
Máme 4 kartičky - jedna kartička s číslem 5 a tři kartičky s číslem 1. Kolik je možností, jak sestavit z kartiček čtyřciferné číslo?
Příklad 117
Máme 4 lístečky. Na dvou z nich je napsaná cifra 7, na druhých dvou cifra 9. Kolik různých čtyřciferných čísel můžeme z kartiček sestavit?
Příklad 118
Máme 5 lístečků. Na třech z nich je napsaná cifra 1, na jednom cifra 2 a na jednom cifra 3. Kolik různých pěticiferných čísel můžeme z kartiček sestavit?
Příklad 119
Kolik existuje různých šesticiferných přirozených čísel, ve kterých se číslice 2 opakuje čtyřikrát a číslice 3 dvakrát?
Příklad 120
Máte dvě černé a dvě bílé kostky. Postavte je na sebe. Vznikne věž, která je vysoká čtyři kostky. Kolik barevně různých věží můžete takto postavit?
Příklad 121
Máme 4 žluté a 5 modrých míčů, které srovnáme do řady. Kolik různých barevných řad takto můžeme vytvořit?
Příklad 122
Na čerpací stanici je v řadě 12 stožárů a 12 vlajek (na každém stožáru je jedna vlajka), 3 modré, 2 zelené, 4 červené a 3 žluté. Kolika různými způsoby lze tyto vlajky umístit na stožáry?
Příklad 123
Kolika způsoby můžeme rozdělit 5 různých bonbónů (všechny bonbóny rozdáme) mezi osm dětí tak, že každé dostane nejvýše jeden bonbón?
| Řešení |
Ukázat |
Když si bonbńy označíme 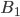 až 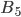 a přidáme k tomu třikrát 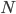 (jako "nic"), tak se vlastně ptáme: "Kolik existuje anagramů slova 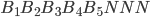 ?" 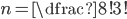
|
Příklad 124
Melodie bude mít 7 tónů, má začínat tónem C a končit tónem G. Třikrát se má použít tón A a dvakrát tón E. Kolik různých melodií je možné vytvořit, když nás zajímá pouze výška tónu, nikoli jeho délka?
Příklad 125
Máme k dispozici 5 dvoumetrových, 4 třítnetrové, 8 čtyřmetrových a 2 sedmimetrové trubky. Kolika způsoby z nich můžeme sestavit potrubí délky 68 m? (Trubky stejné délky jsou nerozlišitelné.)
Příklad 126
K bufetu přijede 21-členný softbalový tým. Hráči si stoupli do fronty a každý z nich si koupil buď sýrový, nebo šunkový sendvič (právě jeden). Kolik různých uspořádání objednávek existuje, když právě 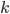 hráčů si koupilo šunkový sendvič?
hráčů si koupilo šunkový sendvič?
Příklad 127
Vlak se skládá ze tří zavazadlových vagónů (nerozlišitlelných), čtyř osobních vagónů s čísly 1 až 4 a dvou lůžkových vagónů s čísly 5 a 6. Kolika způsoby můžeme vlakovou soupravu sestavit, když má začínat vagónem číslo 1 a končit vagónen číslo 6?
Příklad 128
Kolika způsoby můžeme umístit 8 černých a 8 bílých pěšců na šachovnici 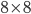 ? Pěšci jedné barvy jsou nerozlišitelní.
? Pěšci jedné barvy jsou nerozlišitelní.
| Řešení |
Ukázat |
Políčka šachovnice si můžeme pojmenovat - běžně se označují "a1" až "h8", tím pádem si je můžeme seřadit do jedné řady. Když si pak označíme umístění bílého pěšce "b", černého "č" a prázdné pole "p", ptáme se vlastně na počet anagramů slova složeného z osmi "b", osmi "č" a 48mi "p". Počet takových anagramů je 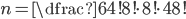
|
Příklad 129
Kolika způsoby můžeme rozmístit šachové figury jedné barvy (bez pěšců) na základní řadu?
| Řešení |
Ukázat |
Při běžném značení šachových figur, hledáme počet anagramů slova složeného ze dvou "V", dvou "J", dvou "S", "K" a "D". 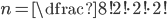
|
Příklad 130
Kolika způsoby můžeme rozmístit všechny šachové figurky (kompletní sadu černých i býlých) na šachovnici?
| Řešení |
Ukázat |
Stejnou úvahou jako příkladu 128. 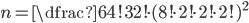
|
Příklad 131
Kolika způsoby můžeme rozmístit 12 černých a 12 bílých hracích kamenů na dámu na černá pole šachovnice  ?
?
Příklad 132
Kolika způsoby lze rozmístit deset knih do tří poliček, když jsou některé knihy rozlišitelné a některé nerozlišitelné (například čtyřikrát „Ferda Mravenec“, třikrát „Malý princ“, dvakrát „Broučci“ a jednou „Bylo nás pět“) a rozlišujeme pořadí, v němž jsou v poličkách srovnány?
| Řešení |
Ukázat |
Knihy si nějak označíme, např. "F", "P", "B" a "5". K tomu přidáme dva symboly pro konec poličky, např. "I". Takže řetězec "FFIPFPFPIBB5" bude znamenat, že v první poličce jsou dva Ferdové, ve druhé dva Ferdové a tři Princové uspořádaní Princ-Ferda-Princ-Ferda-Princ a ve třetí poličce Broučci-Broučci-Bylo nás pět. Každý takový řetězec jednoznačně určuje pořadí knih v poličkách a obráceně každé pořadí můžeme takto zakódovat. Počet anagramů tohoto řetězce je 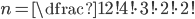
|
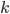 hráčů si koupilo šunkový sendvič?
hráčů si koupilo šunkový sendvič?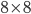 ? Pěšci jedné barvy jsou nerozlišitelní.
? Pěšci jedné barvy jsou nerozlišitelní.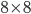 ?
?