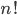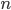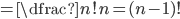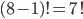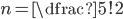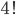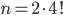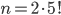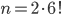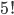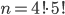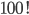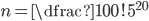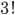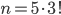kombinatorika

Ve všech příkladech tohoto oddílu považujeme uspořádání, která se na sebe dají převést rotací, za identická.

Příklad 133

Osm lidí tancuje v kruhu. Kolika způsoby můžou být rozestavení?

Řešení	Ukázat
Každé uspořádání do kruhu můžeme někde "rozstřihnout" a tím ho převést na uspořádání v řadě. Přitom platí: "počet uspořádání v řadě" = "počet uspořádání do kruhu" krát "počet přestřihnutí" Protože "počet uspořádání v řadě" je $n!$ a "počet přestřihnutí" je $n$ , je "počet uspořádání do kruhu" $=\dfrac{n!}n=(n-1)!$ Pro zadaná čísla $(8-1)!=7!$

Řešení

Každé uspořádání do kruhu můžeme někde "rozstřihnout" a tím ho převést na uspořádání v řadě. Přitom platí:

"počet uspořádání v řadě" = "počet uspořádání do kruhu" krát "počet přestřihnutí"

Protože "počet uspořádání v řadě" je $n!$ a "počet přestřihnutí" je $n$ , je "počet uspořádání do kruhu" $=\dfrac{n!}n=(n-1)!$ Pro zadaná čísla $(8-1)!=7!$

Příklad 134

Kolika různými způsoby můžeme usadit šest lidí ke kruhovému stolu? Dvě usazení považujeme za stejná, když má každý stejné sousedy bez ohledu na to, zda jsou po levici, nebo po pravici.

Řešení	Ukázat
$n=\dfrac{5!}2$

Příklad 135

Ke kulatému stolu usadíme sedm lidí, mezi nimi Alici, Bětu a Cecílii. Kolik existuje usazení, v nichž má Alice za sousedky Bětu a Cecilii?

Řešení	Ukázat
Alici, Bětu a Cecílii zabalíme do "balíku". Tím máme 5 objektů, které můžeme cyklicky uspořádat $4!$ způsoby. Ale holky v "balíku" můžeme přerovnat dvěma způsoby, takže $n=2\cdot4!$

Příklad 136

Kolika různými způsoby můžeme posadit 7 studentů za kulatý stůl, jestlliže nejvyšší chlapec a nejvyšší dívka mají sedět vedle sebe?

Řešení	Ukázat
$n=2\cdot5!$

Příklad 137

Kolika způsoby se může osm lidí sednou ke kulatému stolu, když Alice a Bob musí sedět vedle sebe?

Řešení	Ukázat
$n=2\cdot6!$

Příklad 138

Kolika způsoby můžeme rozsadit 5 mužů a 5 žen ke kulatému stolu, má-li každá žena sedět mezi dvěma muži?

Řešení	Ukázat
Muže usadíme $4!$ . Jakmile muži sedí, místa mezi nimi jsou rozlišitelná a ženy na ně usadíme $5!$ způsoby. $n=4!\cdot5!$

Příklad 139

Kolika různými způsoby můžeme uspořádat 4 "C" a 2 "H" do kruhu?

Řešení	Ukázat
Třemi způsoby.

Příklad 140

Kolika různými způsoby můžeme usadit 100 lidí ke dvaceti různým kruhovým stolům tak, aby u každého stolu sedělo pět lidí?

Řešení	Ukázat
Lidi seřadíme do řady - to lze $100!$ způsoby - a pak první pětici posadíme k prvnímu stolu, druhou k druhému atd. Ale u každého stolu můžeme otočit při stejném pořadí pětkrát. $n=\dfrac{100!}{5^{20}}$

Příklad 141

Máme klasickou kostku se šesti stěnami. Dále máme 6 barev, kterými obarvíme všechny stěny kostky tak, aby byly všechny stěny různé barvy. Kolik různých obarvení můžeme získat?

Řešení	Ukázat
První barvou můžeme obarvit kostku jedním způsobem. Protilehlou stěnu můžeme pak obarvit pěti způsoby. Zůstaly čtyři barvy na boční stěny, to je $3!$ možností obarvení. $n=5\cdot3!$

Příklad 142

Na hrací kostce musí být součet bodů na protilehlých stěnách 7. Kolika způsoby lze takto očíslovat hrací kostku?

Řešení	Ukázat
Dvěma.

666 příkladů z kombinatoriky

Cyklické permutace