Příklad 377
Určete počet řešení rovnice
kde
a
| Řešení |
Ukázat>
|
Do
přihrádek musíme rozmístit 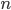
jedniček. Jedná se o kombinace s opakováním. Počet řešení je
|
Příklad 378
Určete počet řešení rovnice
kde
| Řešení |
Ukázat>
|
|
Substitucí
převedeme problém na předchozí případ.
Rovnice má
řešení.
|
Příklad 379
Kolik řešení mají dané rovnice v
?
-
-
-
Příklad 380
Kolik řešení mají dané rovnice v
?
-
-
-
-
-
Příklad 381
Najděte počet řešení rovnice
v množině
když
a současně
| Řešení |
Ukázat>
|
|
Substitucemi
a
převedeme rovnici na základní typ
která má v
řešení.
|
Příklad 382
Kolik různých celočíselných řešení, která splňují
má rovnice
?
| Řešení |
Ukázat>
|
|
Substituce
převedou rovnici na
Ta má v
řešení.
|
Příklad 383
Kolik řešení v lichých přirozených číslech má rovnice
| Řešení |
Ukázat>
|
|
Substituce
převedou rovnici na tvar
pro
Ta má
řešení.
|
Příklad 384
Kolik řešení mají dané rovnice v
?
-
-
-
| Řešení |
Ukázat>
|
|
1. Platí
Musí tedy být
pro
Proto musí platit
Ta má
řešení. Stejný postup i zbývající rovnice.
2.
3.
|
Příklad 385
Pro
určete počet řešení rovnice
| Řešení |
Ukázat>
|
|
Protože
musí být řešení ve tvaru
Počet řešení rovnice
pro
je
Protože výsledek je kladný, musí být v původní rovnici sudý počet znamének "mínus". Pro ně můžeme vybrat pozice
způsoby. Celkem je pak
řešení.
|
Příklad 386
Kolik řešení
rovnice
splňuje podmínku
a
| Řešení |
Ukázat>
|
|
Všech řešení bez podmínek je
Nyní spočítáme opačné jevy:
je množina řešení splňující podmínku
těch je
je množina řešení splňující podmínku
těch je
je množina řešení splňující podmínku
těch je
(z čísel 5 a 7 či větších není možné získat součet 11) a ze stejného důvodu i
Nyní podle PIE je počet vyhovovujících řešení
|
Příklad 387
Kolik řešení pro
má nerovnice
| Řešení |
Ukázat>
|
Musíme sečíst počty řešení rovnic
Podle příkladu 377 je to
Tento výraz můžeme ještě zjednodušit. Vzhledem k tomu, že
můžeme psát
Nerovnice má
řešení.
|
Příklad 388
Kolika způsoby rozložímeme číslo 7 na součet tří přirozených sčítanců? (Na jejich pořadí záleží.)
| Řešení |
Ukázat>
|
|
Podle příkladu 378 je
rozkladů.
|
Příklad 389
Určete, kolik existuje trojciferných přirozených čísel s ciferným součtem rovným 16.
| Řešení |
Ukázat>
|
|
Určujeme počet celočíselných řešení rovnice
s podmínkami (1)
a (2)
(1) po substituci
dostaneme
Tato rovnice má
řešení.
Počet řešení, která nesplňují (2):
Vždy porušuje podmínku (2) jen jeden ze členů.
(a)
substituce
Tato rovnice má
řešení.
(b)
(pro
stejně)
substituce
Tato rovnice má
řešení.
Celkem
čísel.
|
Příklad 390
Kolik je trojciferných čísel, které mají ciferný součet roven 14.
| Řešení |
Ukázat>
|
|
Stejné jako předchozí příklad:
čísel.
|
Příklad 391
Máıne k dispozici pět bonbónů malinových, tři ponıerančové a pět citrónových. Chceme-li si vzít devět bonbónů, kolika způsoby je to možné? (Bonbóny stejného druhu považujeme za nerozlišitelné.)
| Řešení |
Ukázat>
|
|
Řešíme rovnici
s podmínkami
pro
Stejně jako v příkladu 386 budeme postupovat přes opačné jevy.
Všech řešení bez podmínek je
označuje množinu řešení, v nichž
Pak
označuje množinu řešení, v nichž
Pak
Průniky jednotlivých množin jsou prázdné. Ze dvou čísel, z nichž jedno je větší než 5 a druhé větší než 4, nesložíme součet 9. A ostatní možnosti jsou ještě větší.
Celkový počet řešení je
|
Příklad 392
Test se skládá z pěti otázek, každá maximálně za 20 bodů. Student získal postupně 10, 5, 18, 5 a 2 body. Kolika způsoby může opravující přidat studentovi 5 bodů?
| Řešení |
Ukázat>
|
Jedná se o příklad 246 řešený jiným způsobem.
Problém můžeme řešit tak, že určíme počet řešení rovnice
s podmínkou
pro
Počet řešení bez podmínky je
Pro opačný jev
dostaneme rovnici
a ta má
řešení.
Celkový počet řešení je
|
Příklad 393
Určete počet všech pěticiferných čísel dělitelných devíti, jejichž dekadickém zápisu se vyskytují pouze cifry
| Řešení |
Ukázat>
|
Ciferný součet pěticiferných čísel vytvořených z daných číslic leží v intervalu
Protože ciferný součet musí být dělitelný devíti, přicházejí do úvahu jen možnosti
Ale součet sudých čísel je vždy sudý, takže ciferný součet musí být 18. Dále můžeme postupovat tak, že si určíme počet přirozených řešení rovnice
Jelikož je
pro
můžeme rovnici upravit na
pro
a
Rovnice bez podmínky má (příklad 378)
řešení.
Množina
označuje množinu řešení, v nichž
Je
Průniky jednotlivých množin jsou prázdné (nejmenší možný součet
).
Celkový počet hledaných čísel je
|
Příklad 521
Kolik řešení
rovnice
splňuje podmínky
a
| Řešení |
Ukázat>
|
|
Příklad můžeme řešit podobně jako příklad 386 pomocí PIE. Ale je i jiná cesta (ta se dá použít i u příkladu 386).
Představme si, že máme tři přihrádky. Do prvních dvou dáme pět kuliček a do třetí 7 kuliček. Celkem máme nyní 17 kuliček, to znamená, že musíme dvě ubrat. Problém se změnil na otázku "Kolika způsoby můžeme rozdělit dvě "záporné" kuličky do tří přihrádek?" Jedná se o klasický příklad na kombinace s opakováním.
Odpověď:
vhodných řešení.
|