Příklad 357
Nechť
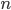 jsou celá nezáporná čísla. Najděte počet cest délky
vedoucích z počátku souřadnicové soustavy do bodu
skládajících se z úseček rovnoběžných se souřadnicovými osami, které mají koncové body v bodech s celočíselnými souřadnicemi.
jsou celá nezáporná čísla. Najděte počet cest délky
vedoucích z počátku souřadnicové soustavy do bodu
skládajících se z úseček rovnoběžných se souřadnicovými osami, které mají koncové body v bodech s celočíselnými souřadnicemi.
| Řešení | Ukázat> |
|---|---|
Příklad 358
Král se má dostat z levého horního rohu šachovnice na obrázku (S) do pravého dolního rohu (F) nejkratší cestou. Kolik takových cest existuje?
| Řešení | Ukázat> |
|---|---|
Příklad 359
Na šachovnici
můžu dělat následující tahy: buď 1 krok vpravo, nebo 2 kroky nahoru. Kolika způsoby se můžu dostat z levého dolního rohu do pravého horního rohu?
| Řešení | Ukázat> |
|---|---|
Příklad 360
Kolik existuje nejkratších cest v celočíselné mřížce z počátku do bodu
jestliže ve směru
se můžeme posunovat jen o sudý počet jednotek?
| Řešení | Ukázat> |
|---|---|
Příklad 361
Kolik existuje nejkratších cest v celočíselné mřížce z počátku do bodu
jestliže ve směru
nesmíme udělat dva kroky bezprostředně za sebou?
| Řešení | Ukázat> |
|---|---|
Příklad 362
Kolik existuje (ne nutně nejkratších) cest z bodu
do bodu
po úsečkách mřížky sestavené z 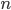 čtverců (viz obr.), jestliže každou úsečku procházíme nejvýše jednou?
čtverců (viz obr.), jestliže každou úsečku procházíme nejvýše jednou?
| Řešení | Ukázat> |
|---|---|
Příklad 363
Baník porazil Barcelonu 7:3.
(a) Kolik různých průběhů mohl mít tento zápas?
(a) Kolik různých průběhů mohl mít tento zápas, jestliže poločas skončil 2:1 ve prospěch Baníku?
| Řešení | Ukázat> |
|---|---|
Příklad 364
Hokejový zápas skončil výsledkem 5:2. Kolik existuje průběhů zápasu, pokud jednotlivé třetiny skončili: 2:1, 2:1, 1:0.
| Řešení | Ukázat> |
|---|---|
Příklad 365
Kolik existuje nejkratších cest v celočíselné mřížce z počátku do bodu
jestliže nejdeme bodem
?
| Řešení | Ukázat> |
|---|---|
Příklad 366
Kolik existuje nejkratších cest v celočíselné mřížce z počátku do bodu
jestliže nejdeme body
| Řešení | Ukázat> |
|---|---|
Příklad 367
Kolik existuje nejkratších cest v celočíselné mřížce z počátku do bodu
jestliže nejdeme úsečkou
?
| Řešení | Ukázat> |
|---|---|
Příklad 368
Na obrázku vidíte plánek města, políčka jsou bloky domů. Kolika způsoby se můžeme dostat z bodu
do
pokud jdeme jen východním nebo severním směrem?
| Řešení | Ukázat> |
|---|---|
Příklad 369
Na obrázku vidíte plánek parku, vyšrafovaná políčka jsou záhony. Kolika způsoby můžeme projít parkem z bodu
do bodu
když půjdeme pouze na jih nebo na západ?
| Řešení | Ukázat> |
|---|---|
Příklad 370
Kolika způsoby se můžeme dostat z bodu do bodu když se můžeme pohybovat jen ve směru šipek?
| Řešení | Ukázat> |
|---|---|
Příklad 371
Po hrací desce, kterou vidíte na obrázku, se pohybuje figurka. V každém kroku se může posunout, jen na sousední tmavší políčko. Kolika způsoby se může dostat z bílého políčka na černé?
| Řešení | Ukázat> |
|---|---|
Příklad 372
Na obrázku vidíte plánek města, vyšrafovaná políčka jsou bloky domů. Zjistěte, kolika způsoby se můžeme dostat z místa
do místa
jestliže:
(a) v každém úseku cesty smíme jít pouze východním nebo jižním směrem.
(b) v každém úseku cesty smíme jít pouze východním nebo jižním směrem a musíme projít přes křižovatku označenou černým křížkem.
| Řešení | Ukázat> |
|---|---|
Příklad 373
Pavouk se pohybuje po drátěném modelu krychle, kterou vidíte na obrázku. Nyní se chce dostat nejkratší cestou z vrcholu
do vrcholu
Kolik různých cest má na výběr? (Smí lézt jen po naznačených úsečkách.)
| Řešení | Ukázat> |
|---|---|
Příklad 374
Fotbalový zápas skončil výsledkem 5:4 pro domácí tým. Domácí se hned v úvodu ujali vedení a udrželi si ho až do konce zápasu. Kolika různými způsoby se mohlo vyvíjet skóre?
| Řešení | Ukázat> |
|---|---|
Příklad 375
Zápas skončil nerozhodně 3:3.
(a) Kolika způsoby se mohlo vyvíjet skóre?
(b) Kolika způsoby se mohlo vyvijet skóre, jestliže domácí nikdy neprohrávali?
| Řešení | Ukázat> |
|---|---|
Příklad 376
Určete počet způsobů, kterými na přiloženém obrázku můžeme vytvořit slovo "ABRACADABRA". Postupovat můžeme vždy jen od jednoho písmene k sousednímu.
| Řešení | Ukázat> |
|---|---|